Adjunction (field theory)

In abstract algebra, adjunction is a construction in field theory, where for a given field extension E/F, subextensions between E and F are constructed.

Definition

Let E be a field extension of a field F. Given a set of elements A in the larger field E we denote by F(A) the smallest subextension which contains the elements of A. We say F(A) is constructed by adjunction of the elements A to F or generated by A.

If A is finite we say F(A) is finitely generated and if A consists of a single element we say F(A) is a simple extension. The primitive element theorem states a finite separable extension is simple.

In a sense, a finitely generated extension is a transcendental generalization of a finite extension since, if the generators in A are all algebraic, then 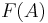is a finite extension of F. Because of this, most examples come from algebraic geometry.

A subextension of a finitely generated field extension is also a finitely generated extension.

Notes

F(A) consists of all those elements of E that can be constructed using a finite number of field operations +, -, *, / applied to elements from F and A. For this reason F(A) is sometimes called the field of rational expressions in F and A.

Examples

• Given a field extension E/F then F(Ø) = F and F(E) = E.
• The complex numbers are constructed by adjunction of the imaginary unit to the real numbers, that is C=R(i).

Properties

Given a field extension E/F and a subset A of E, let 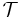be the family of all finite subsets of A. Then

.

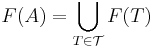In other words the adjunction of any set can be reduced to a union of adjunctions of finite sets.

Given a field extension E/F and two subset N,M of E then K(M ∪ N) = K(M)(N) = K(N)(M). This shows that any adjunction of a finite set can be reduced to a successive adjunction of single elements.